 La teoría de Debye-Huckel establece cómo el campo eléctrico se ve modificado debido a la existencia de otras cargas en disolución.
La teoría de Debye-Huckel establece cómo el campo eléctrico se ve modificado debido a la existencia de otras cargas en disolución.
El ión atrae cargas de signo contrario y repele cargas de igual signo, de modo que su campo eléctrico es, en parte, apantallado. El apantallamiento no es perfecto debido al movimiento térmico
 En un medio de constante dieléctrica εr, el potencial ψ(r) debido un ión de carga ze a una distancia r es, suponiendo que no existe otros iones libres en el medio:
En un medio de constante dieléctrica εr, el potencial ψ(r) debido un ión de carga ze a una distancia r es, suponiendo que no existe otros iones libres en el medio: * en la caso del agua: εr ≈ 80
* en la caso del agua: εr ≈ 80
* e es la carga del electrón (protón): 1.6x10-19 C; z>0 si el ión es positivo y z<0 qi="zie">0 para los iones positivos, zi<0>
• Designaremos por ci la concentración de iones (moles/m3) del tipo i
• Normalmente, cuando se tienen varios tipos de iones en disolución, la carga neta en un punto es cero (se suele decir que la disolución es cuasineutra):

(* cio son las concentraciones de iones cuando no existe campo eléctrico en el medio).
Cuando tenemos el ion de carga ze creando un campo eléctrfico, cerca de este ión la condición de cuasinuetralidad no se verifica y las concentraciones ci de iones son modificadas
En quilibrio términco, las concentraciones ci verifica la ley de distribución Boltzmann:


Integrando sobre las velocidades:

En resumen, para las concentraciones ci de los iones en presencia del potencial ψ debido al ión ze tendremos:

Para determinar ahora el potencial ψ debido al ión ze, usaremos la ecuación de Poisson:
Designando por: F ≡ N = e 96500 C/ mol A
Supongamos que estamos suficientemente lejos del ión ze, de modo que el potencial ψ es suficientemente pequeño para que podamos suponer: zieψ<


 Para encontrar la solución, se realiza el cambio de variable ψ = u/r, que lleva a:
Para encontrar la solución, se realiza el cambio de variable ψ = u/r, que lleva a:

de solución general
 Como ψ debe anularse en el infinito, B=0, y si tenemos en cuenta que en las proximidades del ión ze (r 0) el potencial debe ser culombiano:
Como ψ debe anularse en el infinito, B=0, y si tenemos en cuenta que en las proximidades del ión ze (r 0) el potencial debe ser culombiano:

El parámetro κ recibe el nombre de parámetro de Debye-Huckel:
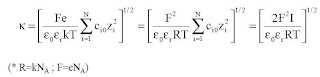
Es la denominada fuerza iónica
El potencial debido al ión ze queda prácticamente apantallado por la nube de iones en una longitud característica 1/κ, denominada longitud de Debye-Huckel o radio de Debye-Huckel

 * Efecto sobre el potencial ψ de una nube iónica formada por una sola especie iónica con z=1, para diversos valores de la concentración de dicha especie.
* Efecto sobre el potencial ψ de una nube iónica formada por una sola especie iónica con z=1, para diversos valores de la concentración de dicha especie.
Ejemplo: consideramos una disolución con la siguiente composición:
105 mM ClNa, 5 mM ClK, 25 mM PO4HNa2, 2 mM Cl2Ca
Consideramos las sales completamente disociadas.
La fuerza iónica I será:
 y el radio de Debye-Huckel, a temperatura ambiente T=298 K
y el radio de Debye-Huckel, a temperatura ambiente T=298 K









No hay comentarios:
Publicar un comentario